Sorting
Data structure and algorithms are two important courses in Computer Science. Knowing how to utilise appropriate data structures and algorithms to fit our problems can greatly decrease memory space and improve performance. Besides, the ideas behind the classical algorithms are also worth learning to strengthen our logical thinking skills. Well, this series of articles are simply quick notes to help refresh my knowledge for future reference. So let’s start from sorting.
Bubble Sort
Idea
Bubble sort is the first sorting algorithm I learned in the module ‘Data Structure’. The idea is simple,
each time, we compare numbers in pairs and make an exchange until we put the largest number at the rightmost position
Say we have $n = 6$ numbers shown in Figure 1,

For the first iteration, there are n = 6 items left to sort, so we need to compare n - 1 = 5 pairs of elements consecutively.
(9, 4), 2, 16, 10, 12
4, (9, 2), 16, 10, 12
4, 2, (9, 16), 10, 12
4, 2, 9, (16, 10), 12
4, 2, 9, 10, (16, 12)
Similarly, for the second loop, there are n - 1 = 5 items left to sort, and we need to compare n - 2 = 4 pairs of elements.
(4, 2), 9, 10, 12, 16
2, (4, 9), 10, 12, 16
2, 4, (9, 10), 12, 16
2, 4, 9, (10, 12), 16
From this, we can conclude that, for the $i\text{th}$ loop,
- there are $n - i$ items left to sort
- consequently, we need to compare $n - i - 1$ times
Since we place the largest number at the rightmost position for each loop, so there are $n-1$ loops in total. The following table shows the above procedure.
| iterations | times we need to compare |
|---|---|
| 0 | n - 1 |
| 1 | n - 2 |
| 2 | n - 3 |
| … | |
| n - 2 | 1 |
Code
def bubbleSort(nums):
n = len(nums)
for i in range(n - 1): # each loop
for j in range(n - i - 1):
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
return nums
bubbleSort([9, 4, 2, 16, 10, 12])
# [2, 4, 9, 10, 12, 16]
Analysis
Stable - Yes
Since we only swap values when the previous item is greater than the latter item, the items with the same values will keep their order.
Complexity - O($n^2$)
From the table above, we can see that,
- in the worst case, we need to run comparison $1 + 2 + … + (n - 1) = \frac{(n-1)n}{2}$ times
- in the best case, we still need to compare $\frac{(n-1)n}{2}$ times
In this example, we notice that 2, (4, 9), 10, 12, 16 have been in order, but the comparison continues. One way is to set a flag to notice it. We can do this because Bubble Sort is an in-place sorting, which means the list has sorted in ascending order while comparing.
def bubbleSort(nums):
n = len(nums)
has_sorted = False
for i in range(n - 1): # loop passes
if has_sorted:
break
for j in range(n - i - 1):
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
has_sorted = False
else:
has_sorted = True
return nums
Now the complexity of the enhanced Bubble Sort for the bset case is $O(n)$ while the worset case still stays the same.
Selection Sort
Idea
Selection sort is similar to Bubble sort. It first finds the index of the largest value in the remaining list, then makes an exchange between the largest item and the rightmost item for each loop. Therefore, the exchange happens only once in each iteration.
Like Bubble sort, there are $n - 1$ iterations. For each iteration, we need to find the largest value from the remaining $n -i$ items.
Code
def selectionSort(nums):
n = len(nums)
for i in range(n - 1):
max_index = 0
for j in range(1, n - i):
if nums[j] > nums[max_index]:
max_index = j
nums[n-i-1], nums[max_index] = nums[max_index], nums[n-i-1]
return nums
Analysis
Stable - No
After each iteration, we swap two items, so the order of the items are not ensured.
Complexity
Obviously, no matter the best case or the worst case, we need $O(n^2)$ comparisons.
Insertion Sort
Idea
As the name suggests, we insert an item into the proper position of the well-sorted sublist each time. In other words, we maintain the sublist sorted in each iteration.
But how? For each $x_i$ in the sorted list, we compare $x_i$ with the being sorted item $x'$,
- if $x' >= x_i$,
- simply put $x'$ behind $x_i$
- end
- if $x' < x_i$,
- move $x_i$ a step forward (in the right direction)
- then move on to the next $x_i$ in the sorted list
- repeat the above comparison
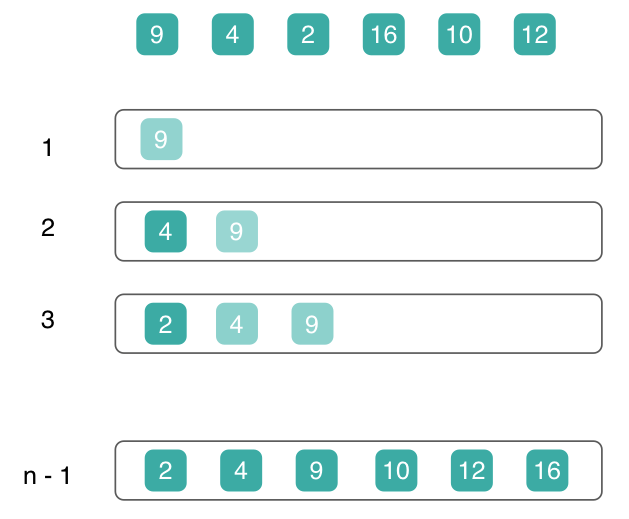
- or we reach the start point, then we know that $x'$ is the smallest number so far. For example, $2$ is placed at the beginning of the list during the third iteration shown in Figure 2.
Code
def insertionSort(nums):
n = len(nums)
for i in range(1, n):
cur_elem = nums[i]
cur_index = i
while cur_index > 0 and cur_elem < nums[cur_index - 1]:
nums[cur_index] = nums[cur_index - 1]
cur_index -= 1
nums[cur_index] = cur_elem
return nums
Analysis
Stable - Yes
Complexity
For the best case where all items are sorted well and the corresponding sublist is sorted, there is no need to do a move operation. Therefore, the complexity is $O(n)$.
For the worst case, we still need $O(n^2$) comparisons.
Quick Sort
Idea
Quick sort adopts the idea of divide and conquer. The main strategy is that we do a partition at the pivot value, dividing the list into two parts
- the left part contains items that are smaller than the pivot value
- the right part contains items that are greater than the pivot value
How? Well, we use two pointers: the left pointer and the right pointer that point to the first and the last of the remaining list respectively.
- Move the left pointer forward(towards the right direction) until the pointed element is greater than the pivot value
- Move the right pointer backward(towards the left direction) until the pointed element is smaller than the pivot value
But how to choose the pivot? Well, you could use the first element of a list.
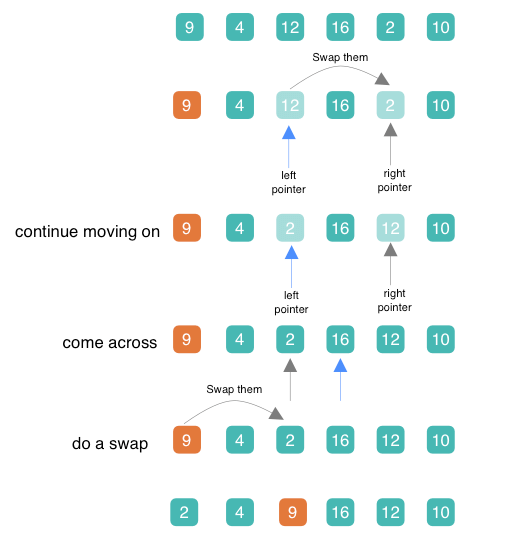
Let’s take an example. In Figure 3, we choose 9 as our pivot, after some steps we stop at the second row. We do a swap between pointers and then continue moving on until the two pointers pass by each other (the forth row). Well, since the two pointers have met, we cannot move further towards either the right or the left direction, which means that we are done. Obviously, the pivot value should be between the right pointer and the left pointer, so we do an exchange again.
Analysis
Stable - No
We do a swap between pointers, so the order of elements are not maintained.