Bias-Variance dilemma
When you learn more about machine learning, you must hear people talking about high bias, high variance or something like that. What do they mean by ‘high bias’ or ‘high variance’?
Actually, when I first heard these terms, I was completely confused. Even though I tried to find the answer on Google, I still had no idea until I took the Advanced Machine Learning module in semester 2. Therefore, I’m writing this post to try to explain this. I hope this post can help people who are still struggling with them to understand the two most important concepts clearly.
Generalization Error
The underlying assumption of machine learning is that there are some relationships between data. However, we are not able to know this true function, otherwise there is no need to learn it.
Suppose we have a true realtionship denoted by $f(x)$ (the red dot in Figure 1), and we want to construct a machine denoted by $f'(x)$ to approximate the true function based on the data $D$ sampled from the population $\chi$.
The training loss is defined by the following equation, where $f'(x|D)$ is the machine we learn from this particular data set $D$
$$ L_T(D) = \sum_{x\in D}(f'(x|D) - f(x))^2 $$
However, our goal is to know how well this machine works on unseen data, which is known as generalization. The generalization loss is expressed as
$$ L_G(D) = \sum_{x\in \chi} p(x) (f'(x|D) - f(x))^2 $$
If we have another data set $D_1$, then we will get another machine $f'(x|D_1)$ and another generalization loss $L_G(D_1)$ shown in Figure 1.
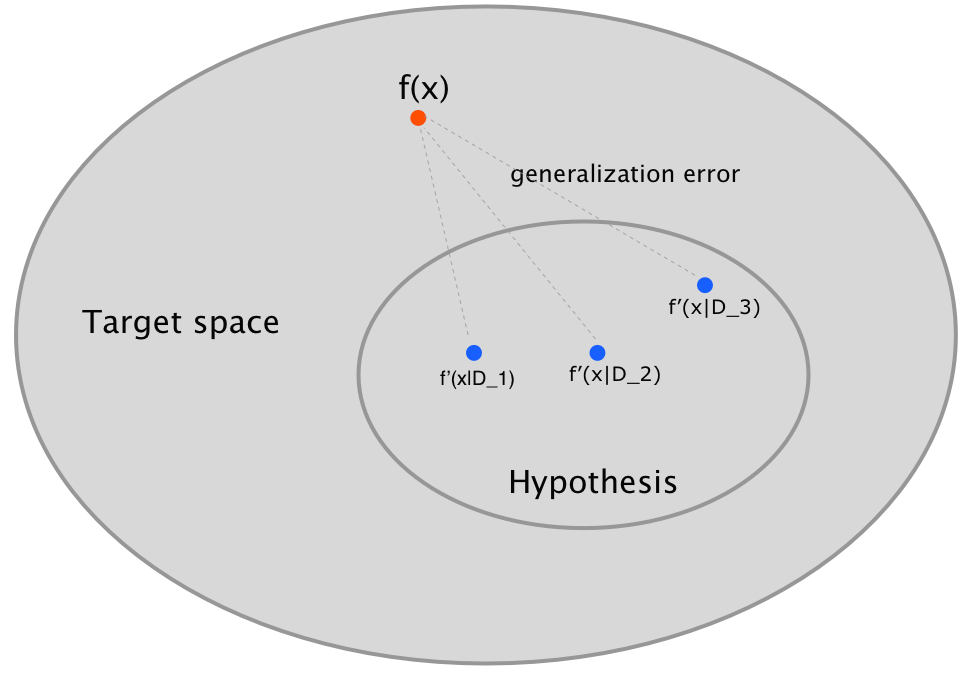
We can see that the generalization loss is depend on our training data. Thus, the generalization loss for a particular data set doesn’t make much sense. Instead, the average generalization loss over all the data set with the same size of $n$ is what we expect.
$$ E_G = E_D[L_G(D)] = E_D[\sum_{x\in \chi} p(x)(f'(x|D) - f(x))^2] $$
Mean Machine
We have already known that there is a different machine $f'(x|D)$ for a given data set $D$. Thus, for an unseen data $x$, we will have many predictions of many different machines, which are represented in blut dots shown in Figure 2.
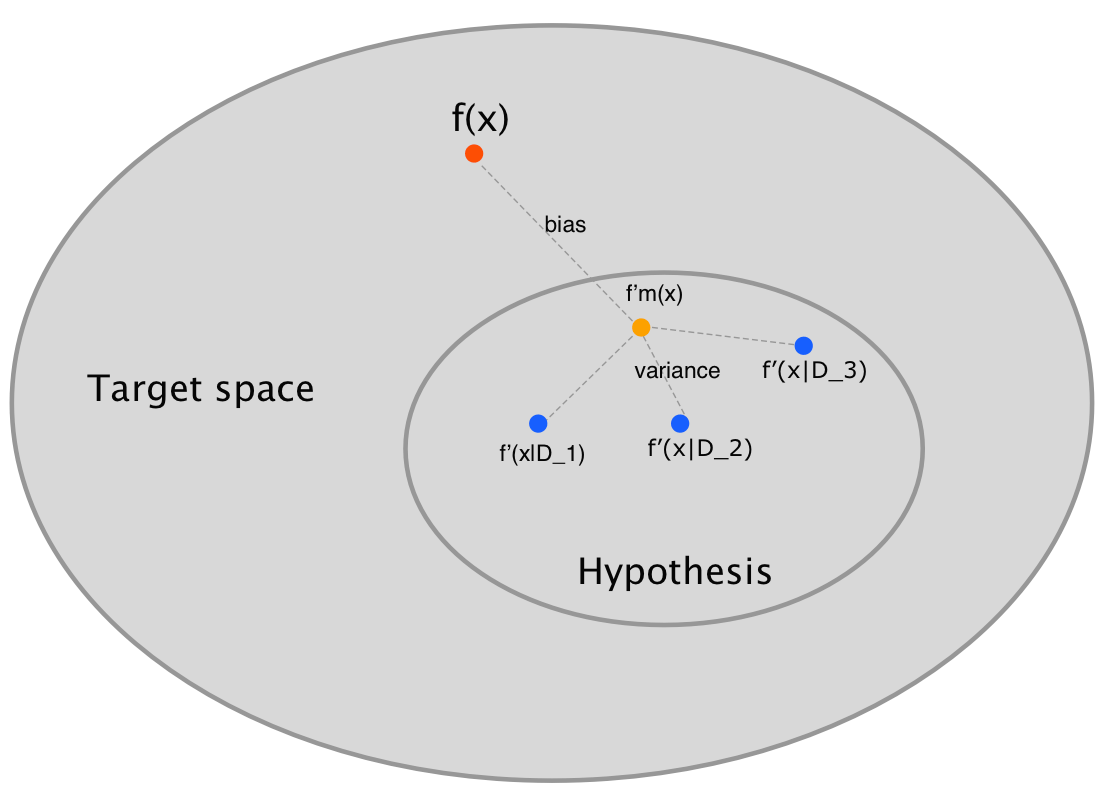
The average prediction for an unseen data is the mean prediction(the yellow dot in Figure 2).
$$ f'_m(x) = E_D[f'(x|D)] $$
Bias
Bias is the distance between the mean prediction(the yellow dot) and the true value(the red dot) shown in Figure 2. High bias implies that our model is too simple and the prediction value is much far away from the true value.
$$ B = \sum_{x \in \chi} p(x) (f’m - f(x))^2 $$
Variance
Variance measures the variation in the prediction of the machine when we change different data set we train on. If we have a complex machine, as mentioned earlier, the machine will try its best to match every data in training data set. In other words, the machine memorized the trainining data and a little change in data set will cause significant variation in prediction.
$$ V = \sum_{x \in \chi}p(x) E_D[ (f'(x|D) - f’m)^2 ] $$
Bias-Variance dilemma
Now it’s time to decompose the average generalisation error. Let’s plug the $f'_m(x)$ into the previous equation
$$ E_G = E_D[L_G(D)] = E_D[\sum_{x\in \chi} p(x)(f'(x|D) - f(x))^2] $$
$$ = E_D[\sum_{x\in \chi}p(x) (f'(x|D) - f_m' + f_m' - f(x))^2] $$
$$ = E_D[\sum_{x\in \chi}p(x){(f'(x|D) - f_m')^2 + (f_m' - f(x))^2 + 2(f'(x|D) - f_m')(f_m' - f(x)) }] $$
It’s noticeable that the cross-term will cancel out because $f’m$ and $f(x)$ are constants no matter what data set $D$ is.
$$ E_D[\sum_{x\in \chi}p(x)2(f'(x|D) - f_m')(f_m' - f(x))] $$
$$ = \sum_{x\in \chi}p(x) (2E_D[f'(x|D)]-f’m)(f’m-f(x)) = 0 $$
Therefore, we are left with
$$ E_G = E_D[L_G(D)] = E_D[\sum_{x\in \chi}p(x)(f'(x|D) - f_m')^2 + \sum_{x\in \chi}p(x)(f_m' - f(x))^2] $$
$$ = \sum_{x\in \chi}p(x) E_D[(f'(x|D) - f_m')^2] + \sum_{x\in \chi}p(x)(f_m' - f(x))^2 $$
$$ = V + B $$
In summary,
- If our machine is too simple, then we might not be able to fit the training data. Since the machine knows little about the data, it’s unlikely to work well on unseen data. This means our model has a high bias.
- If our machine is too complex, then we might be able to fit the training data perfectly. It means that the machine knows too much about the data, even the noise that it should not learn. Thus, it’s too sensitive to training data so that a little change in data will cause a great variance. This means our model has a high variance.
Throughout the world of machine learning, we are always trying to find a balance between bias and variance.