K-nearest neighbours
K-Nearest Neighbors(KNN) is a distance-based algorithm in machine learning used for both classification and regression. It’s simple and intutive to understand because it doesn’t require extra training step and the idea behind it is simple enough — similar points are tends to be close to each other. In this article, we will learn how KNN works.
How KNN works
Suppose we have a dataset and a new data point, we want to know which class this new example belong to or what the predicted value is if it’s a regression task. KNN works in this way,
- Choose a value for $K$
- Calculate distances between the new point and each sample of the training data
- Sort the distances from the nearest to farthest and get the first $K$ nearest samples
- For classification
- Majority vote among the $K$ observations. The new sample belongs to class that has the highest votes.
- For regression
- Average the value of the $K$ observations
def majority_vote(labels):
votes = Counter(labels)
label, _ = votes.most_common(1)[0]
return label
def knn_classify(inputs, labels, x, k, distance):
distances = sorted([ (distance(x, point), label)
for point, label in zip(inputs, labels)],
key=lambda: lp:lp[0])
k_nearest_labels = [ lp[1] for lp in distances[:k] ]
return majority_vote(k_nearest_labels)
What if we have the same votes for two different categories?
- Pick one of them randomly
- Calculate weighted voting
- Reduce k until we find a unique answer
Distance
From above, we can see that the main problems are how to find an appropriate $K$ and how to measure distance. There are several common distance measures in machine learning, such as Euclidean and Manhattan. They are applied in different situations, so knowing how and when they can be best used is important to improve our model performance.
Euclidean Distance
Euclidean distance is defined as follows,
$$ D = \sqrt{\sum_i^d (x_i - y_i)^2} $$
It’s simply the length of the straight line connecting two points. We should be careful with it because it’s sensitve to the scale of features. So we need to normalize data first. Besides, it is not suitable for high-dimensional space. Anyway, it’s still the most common and straightforward distance measure.
Cosine Distance
Cosine distance measures the closeness between two points by calculating the angle between them.
$$ D = \text{cos}\theta = \frac{x \cdot y}{||x|| \text{ } ||y||} $$
So this method doesn’t care about the length of a vector. If we are more interested in the direction of a vector rather than the length, it would be a better choice. For example, two documents represented by word-document vector could be similar even they vary in the number of the same words. This might be because one document is just much longer than another one, but they are all related to the same topic.
Manhattan Distance
Manhattan distance is defined as the sum of steps moving from one point to another point. You can only move along the horizontal direction or vertical direction. Imagine you stand on a chess board, how many cells do you need to move?
$$ D = \sum_i^d |x_i - y_i| $$
This method originated from how to calculate the distance between source and destination in a city. You cannot always walk through a building or something, so Euclidean distance is not helpful. Instead, a distance based on streets would be optimal.
Through Manhattan distance could work well in a high-dimensional space, it’s less intutive than Euclidean distance. Also, the distance measured by Manhattan is a bit larger than Euclidean because of the Triangle Inequality Theorem.
Finding the best K
How do we find the optimal value for $K$? If $K$ is too small, the model would have a high variance and a poor generalization. If $K$ is too large, the model would have a high bias.
- If we have some domain knowledge, for example, we want to classify whether a new flower belong to a specific species among given all species. $K$ could be the number of that specific species.
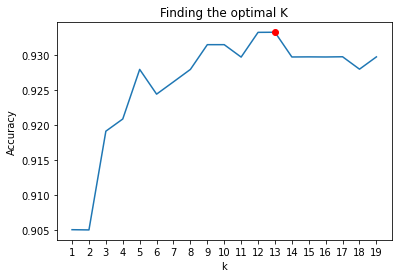
- Typically, we may have little domain knowledge, one way to find the best $K$ is cross-validation. We choose the ‘elbow’ point as the optimal $K$ from all these scores returned by cross-validation, as shown below.
- As a rule of thumb, we could choose $k = \sqrt N$, where $N$ is the number of samples
Pros and Cons
Pros
- Easy, simple and straightforward to understand
- no need to train, it’s a non-parametric method
- Suitable for both classification and regression
Cons
- More suitable for a small number of samples because distance is computed throughout nearly every data in the training set. Thus computation might be a matter if the dataset is large.
- Sensitive to outliers. If one category has some outliers, a new sample might be classified into this category since they might be more close to the new sample even if the new sample should belong to another category.
- Tends to be biased if samples are unbalanced. One category would dominate the majority voting of the new sample because it has a great number of samples.